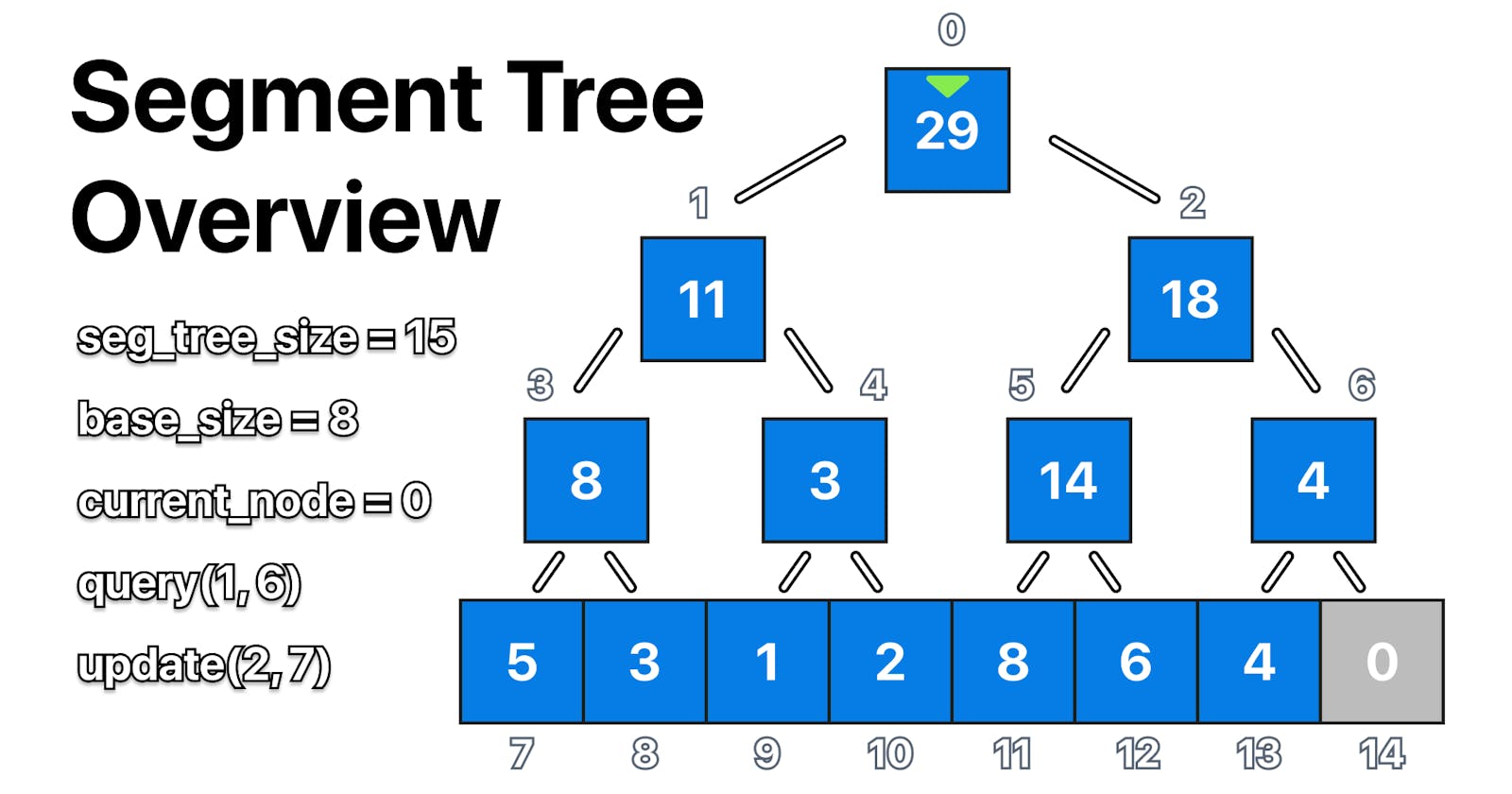
Introduction
Welcome Back! In this post, we will take a beginner's dive into segment trees in c++, we will look at what are they. what are they for? and we will solve some basic competitive programming problems together.
Before we begin, I highly suggest that you check out my post about Efficiency And Big O Notation altho it is not required 😉.
What is a Segment Tree?
Segment Tree is one of the most used data structures in competitive programming, to understand why they are such a big deal, let's think of the following problem:
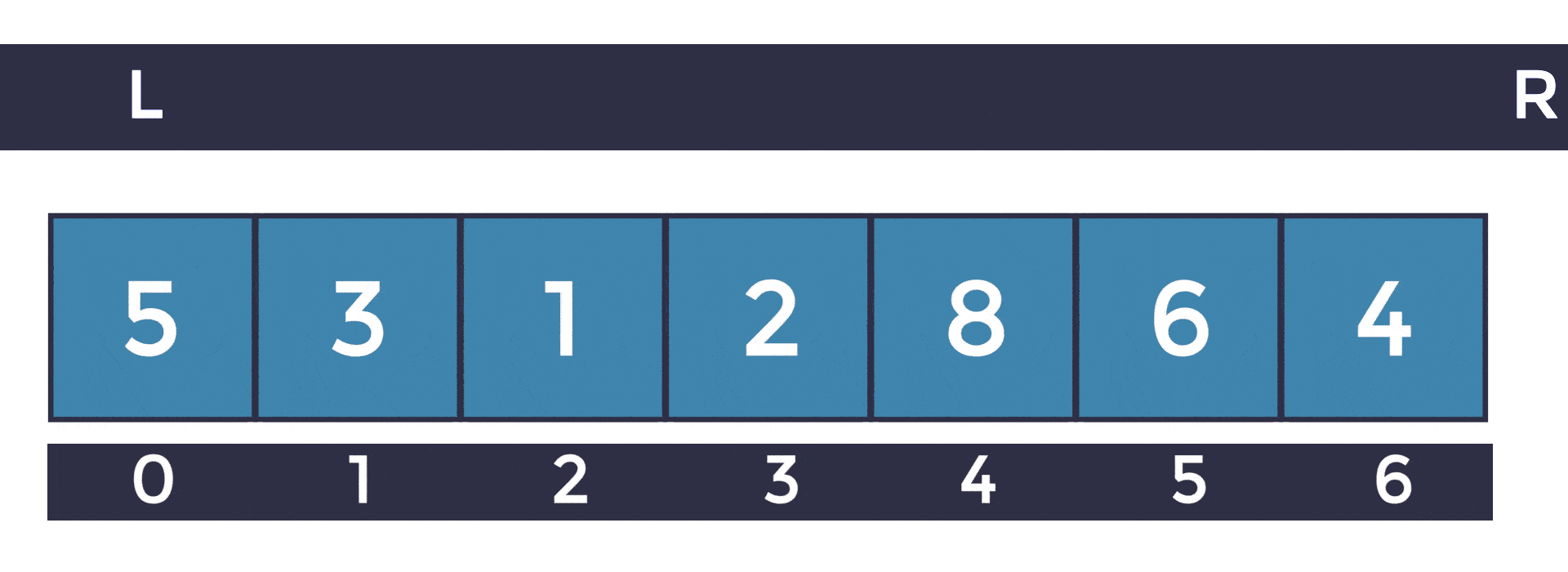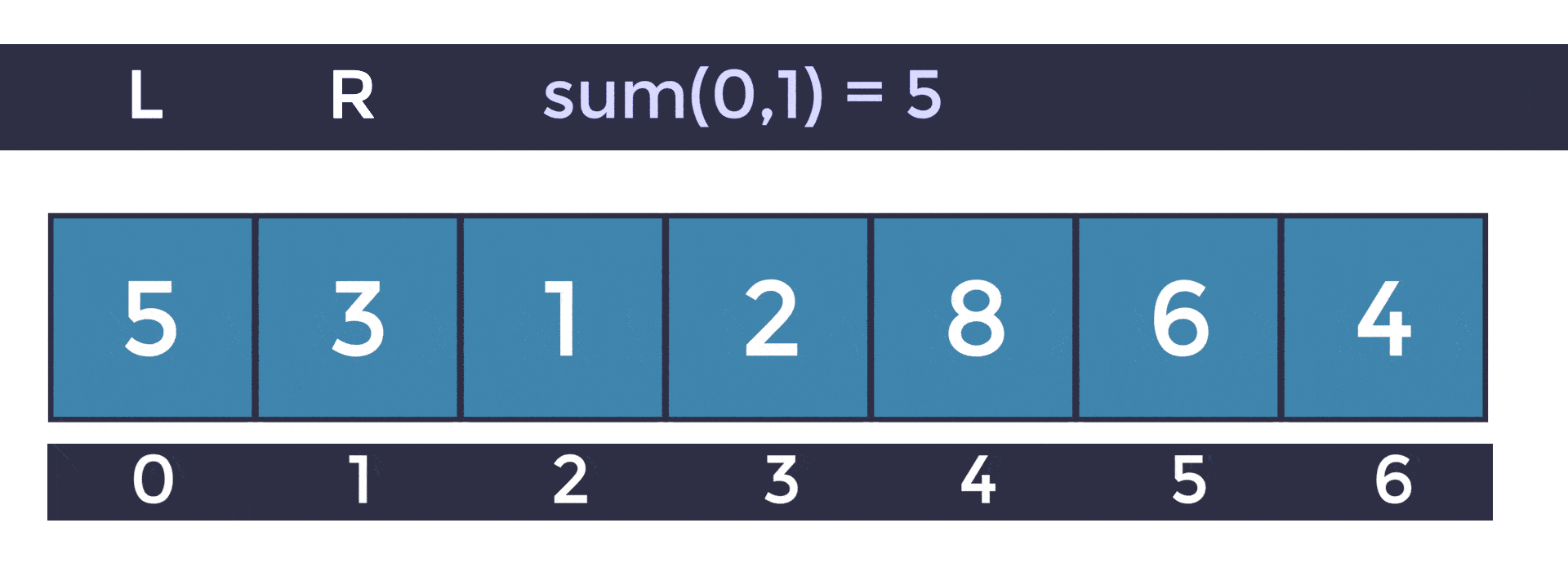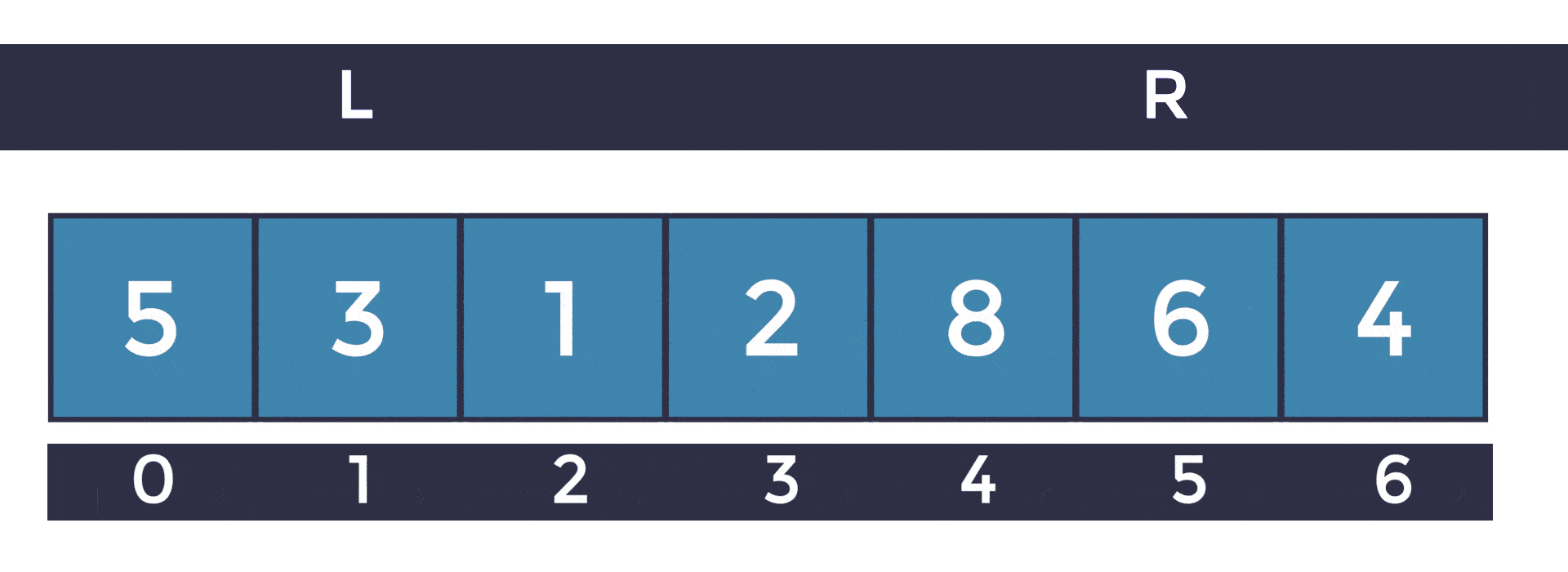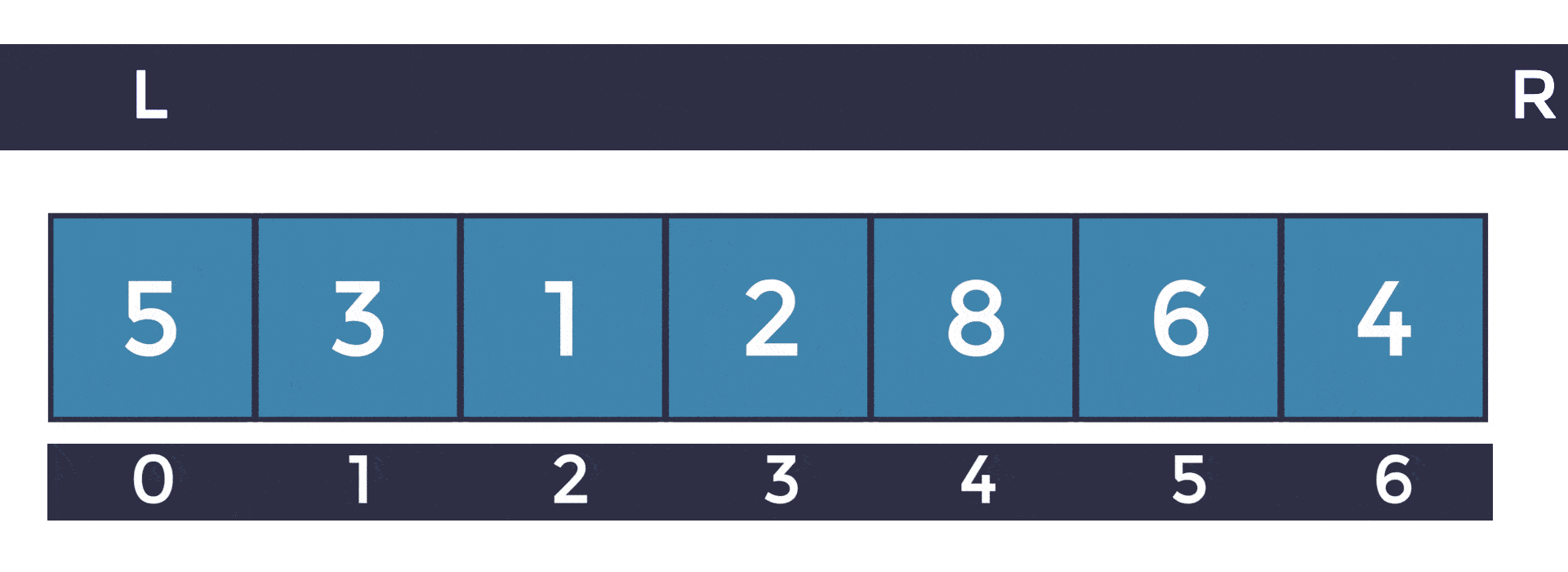
Let's say we have an array of N elements, like the one shown below:
And we need to perform two types of operations. The first operation will be an update(i, v), this function will take the index of the element we want to change, and the new value, and replace it.
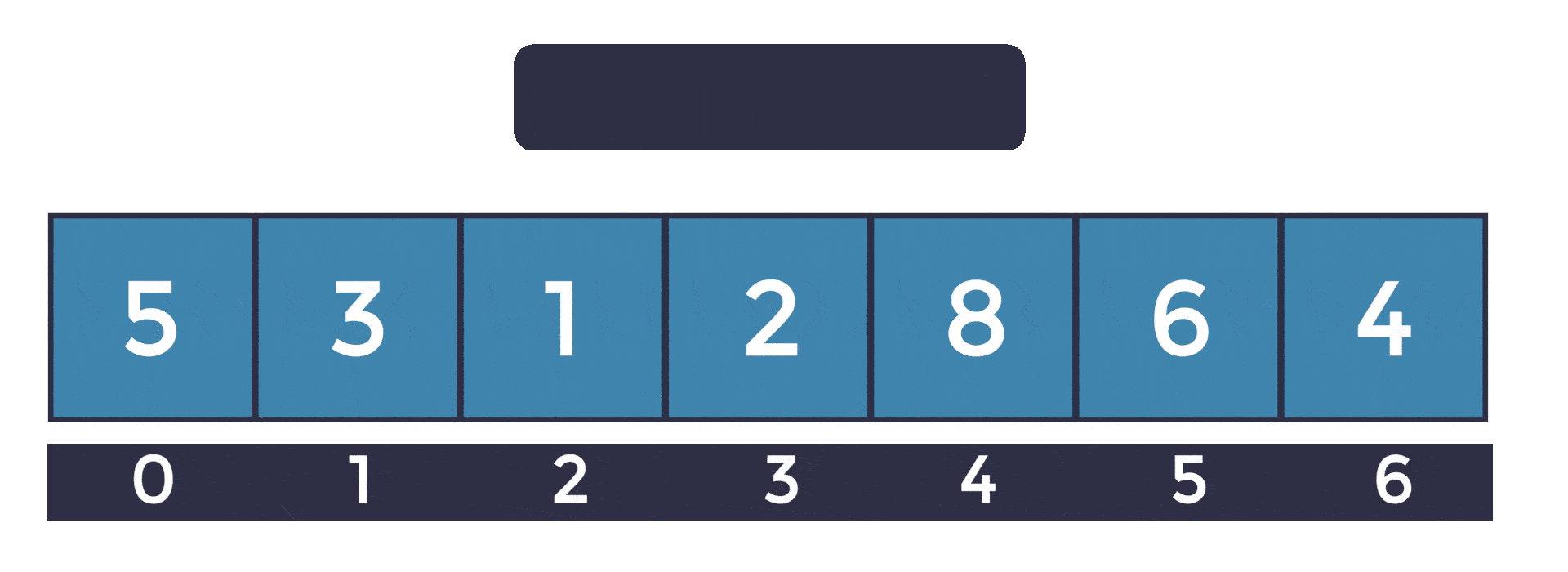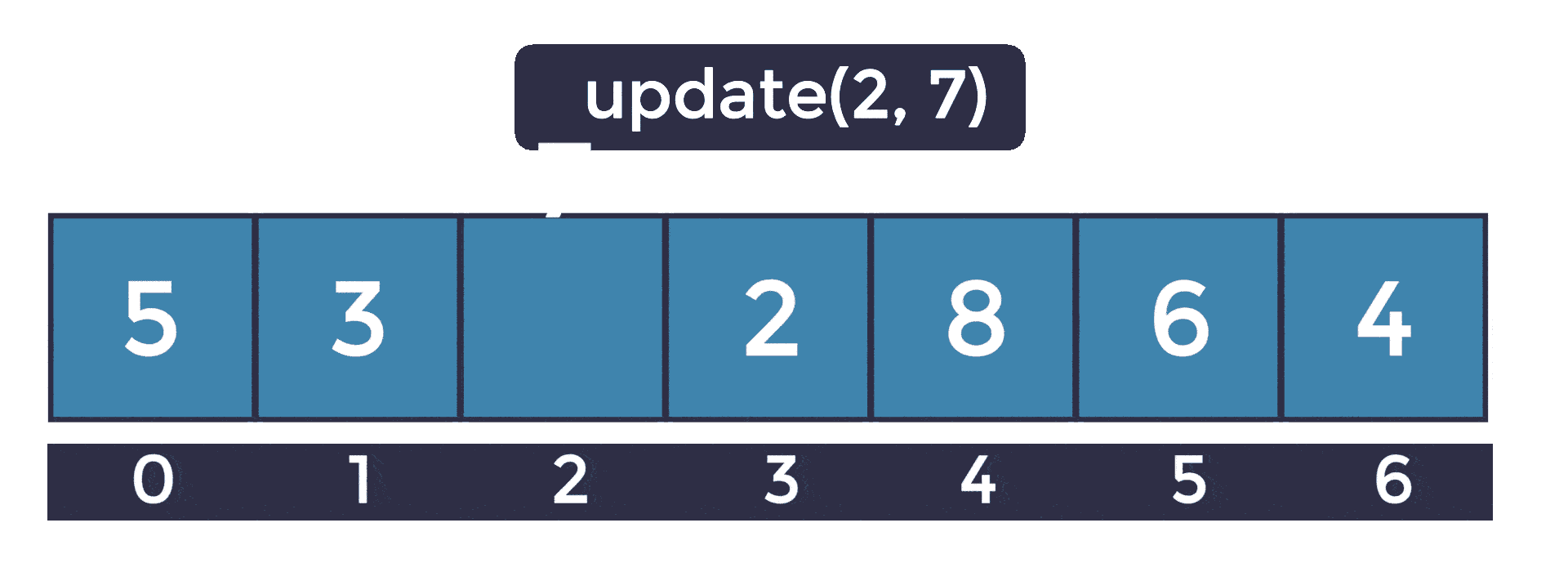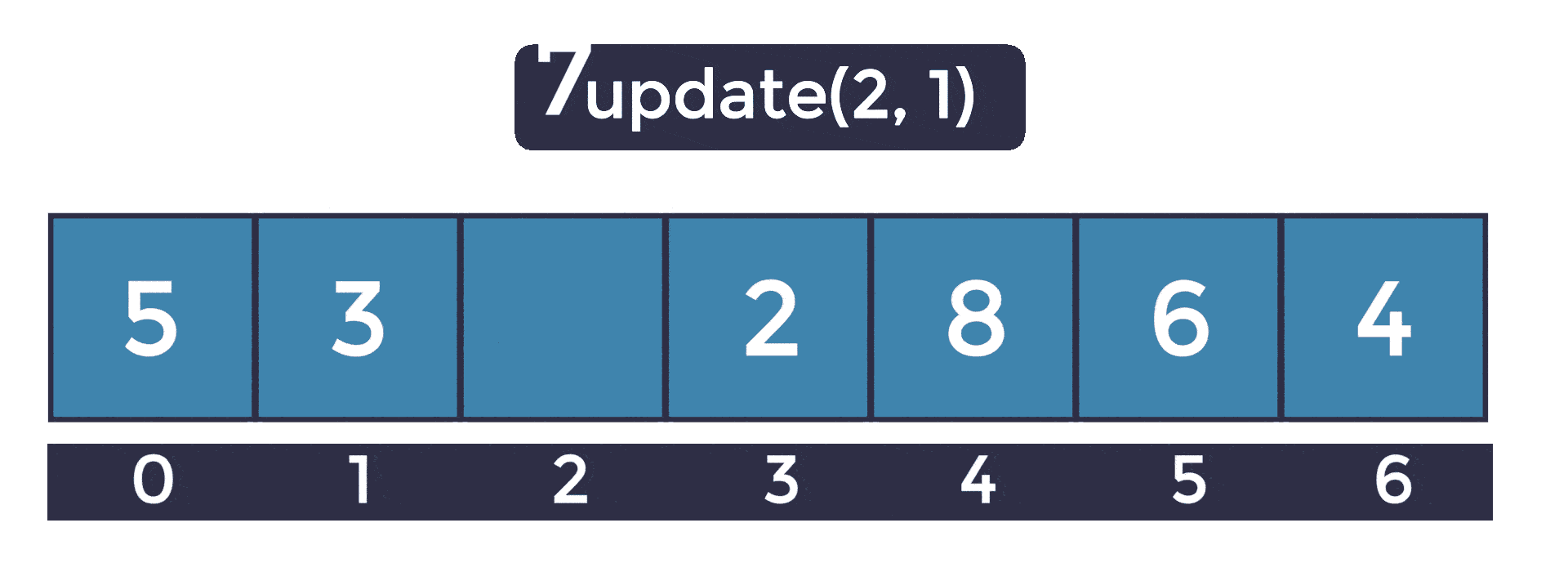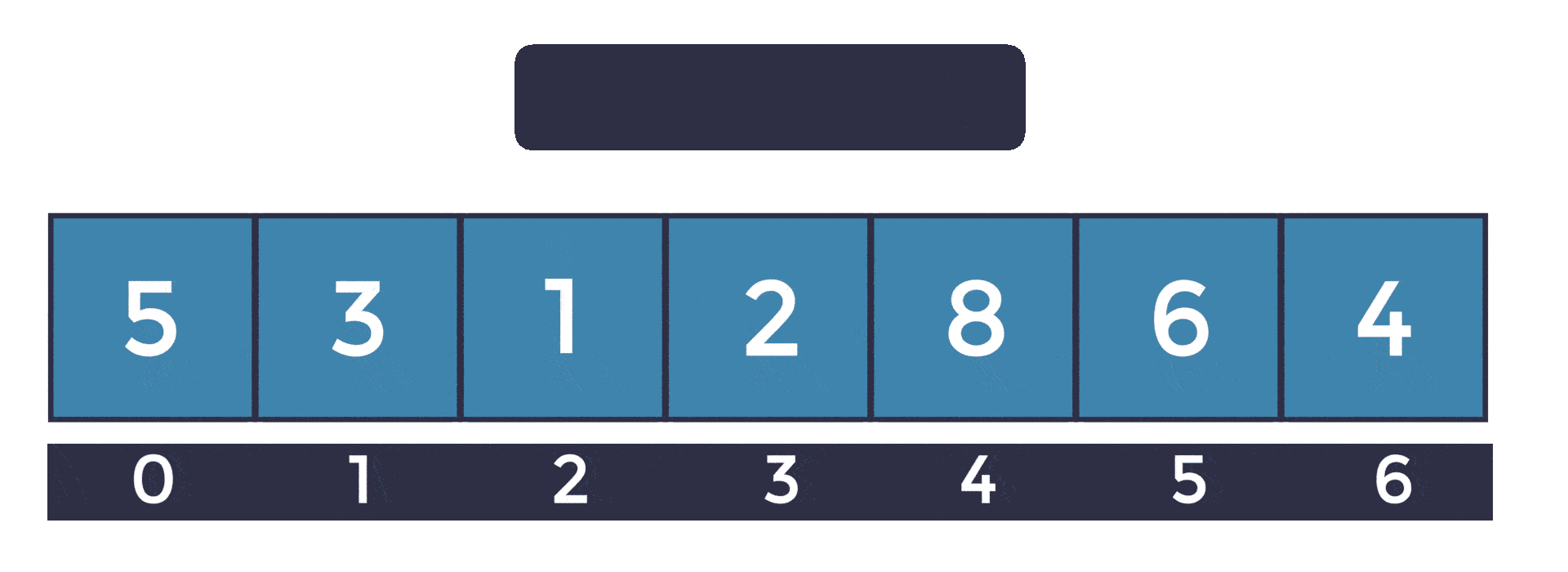
The second operation is going to calculate to sum in a segment a.k.a range in the array from [ L to R) Note that in the request for the sum we take the left border [ L inclusive, and the right border R ) exclusive. In this post, we will follow this inclusive exclusive standard for all segments. Here are some examples of the sum(l, r) in action:
A Segment tree is a data structure that will allow us to perform both of the operations in log(n) time complexity, we will look more in detail at how this works, but before we continue, let's see how we could solve this problem only using iteration.
Iterative Solution
Let's think of the most basic solution that does not involve a segment tree first. In the code cell below, we define a vector globally for commodity reasons, and we receive the input N, then we resize the vector to the given size and store the data from the terminal.
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int n;
vector<int> arr;
int main() {
cin >> n;
arr.resize(n);
for (auto &e : arr) cin >> e;
return 0;
}
Define sum() Procedure
As you can see from the code cell below, this method is very simple, we simply iterate the array using a for loop, starting from a to b-1, notice how we don't have to subtract 1 to b because we use "<" instead of "<=", and sum all the values to the result variable.
int sum(int a, int b) {
int result = 0;
for (int i = a; i < b; i++) result += arr[i];
return result;
}
Define update() Procedure
This function is the easiest to implement because we only need the following line of code:
void update(int index, int new_value) { arr[index] = new_value; }
The Update method does not return anything, that's why we use void(), and we don't need to pass the array as a parameter because it's defined globally.
Testing Solution
Feel free to copy the code locally on your machine and test it out!
int main() {
cin >> n;
arr.resize(n);
for (auto &e : arr) cin >> e;
cout << sum(0, 7) << endl;
cout << sum(0, 1) << endl;
cout << sum(1, 6) << endl;
update(0, 10);
cout << sum(0, 7) << endl;
cout << sum(0, 1) << endl;
cout << sum(1, 6) << endl;
return 0;
}
Expected output:
29 5 20 34 10 20
Time - Space Complexity
After coding the iterative solution, you must be thinking: "Hey!, this was easy to code, why don't we just use this approach?", and yes! that solution is simple and easy, but is it efficient? for example what happens if you have the following limits?:
- (1≤N≤10^5, 1≤M≤10^5) where N is the number of elements, and M is the number of operations that are going to be performed.
Update() Time Complexity
Surprisingly, the update procedure takes O(1) constant time, which means it's super efficient!
Sum() Time Complexity
However, this procedure has a worst-case scenario of O(N) this is the case if we ask for a range from 0 to N, the problem is that there can be up to 10^5 of this type of function calls
sum(0, 1E5)
sum(0, 1E5)
sum(0, 1E5)
sum(0, 1E5)
sum(0, 1E5)
... 10^5 more times
and for every call, we have to iterate the entire array even tho the array stays the same. Because of this, this procedure has a complexity of O(N*M) and because in this case N and M can be the same worst-case value, we say that this solution has a complexity of O(N²) which is not efficient at all!
Segment Tree Solution
Structure of the segment tree
Starting from the previous example array, let's see what a segment tree would look like for this particular array.
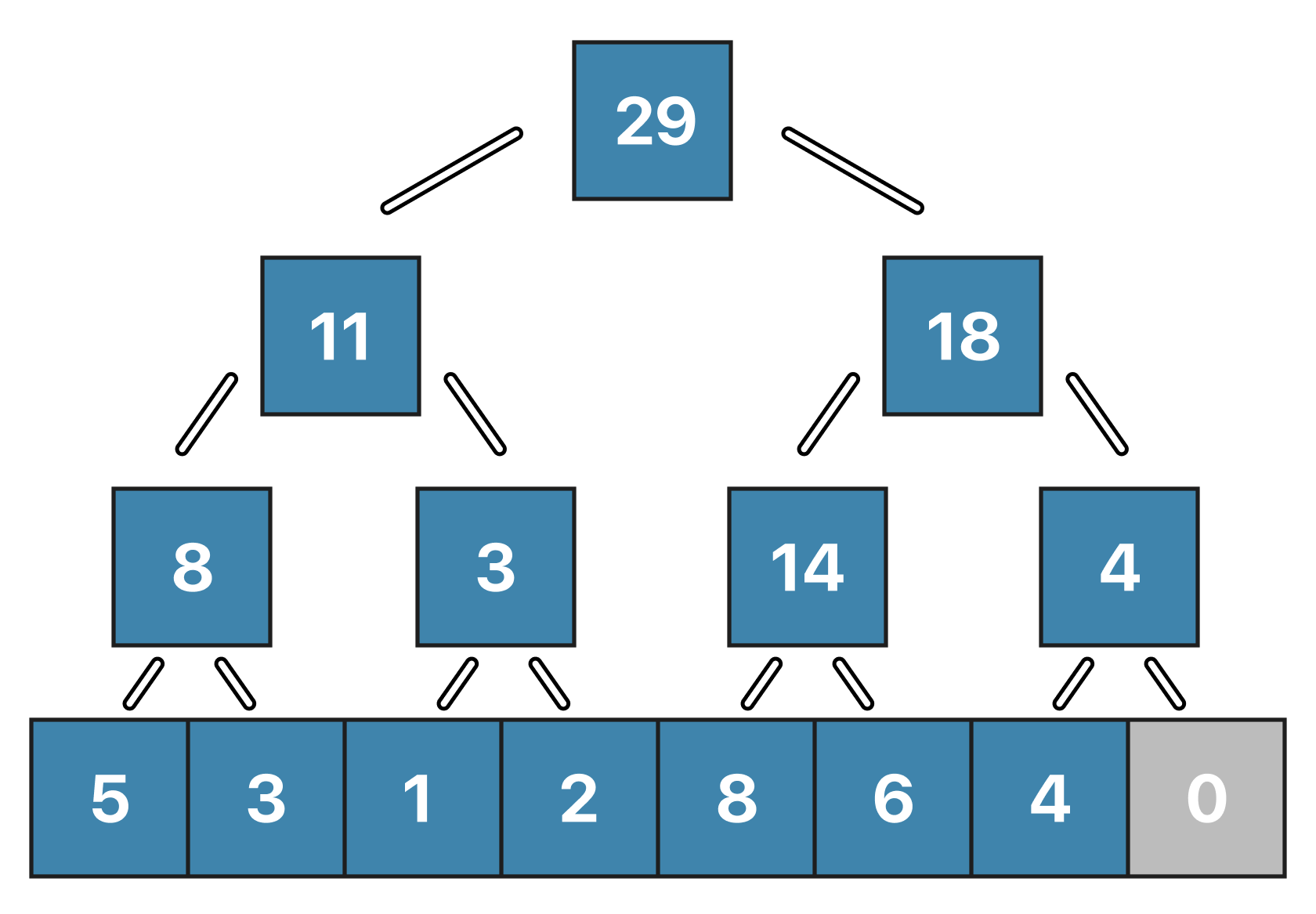
This is a binary tree, in the leaves of which there are elements of the original array, and each internal node contains the sum of the numbers in its children.
notice how we added a 0 at the end of the original array because we need to create a Binary Tree, and for the tree to be created perfectly we need the length of the array to be a power of two. If the length of the array is not a power of two, you can extend the array with a neutral value, in this case, a 0, notice how the length of the array will increase no more than twice, so the asymptotic time complexity of the operations will not change.
Now let's see how the operations will look on this tree.
Update() Operation
When an element of the array changes, what we need to do is traverse the tree until we reach the corresponding leave of the tree, then update the value, and recalculate all the values higher up the tree from the modified leaf. When performing such an operation, we need to recalculate one node on each layer of the tree.
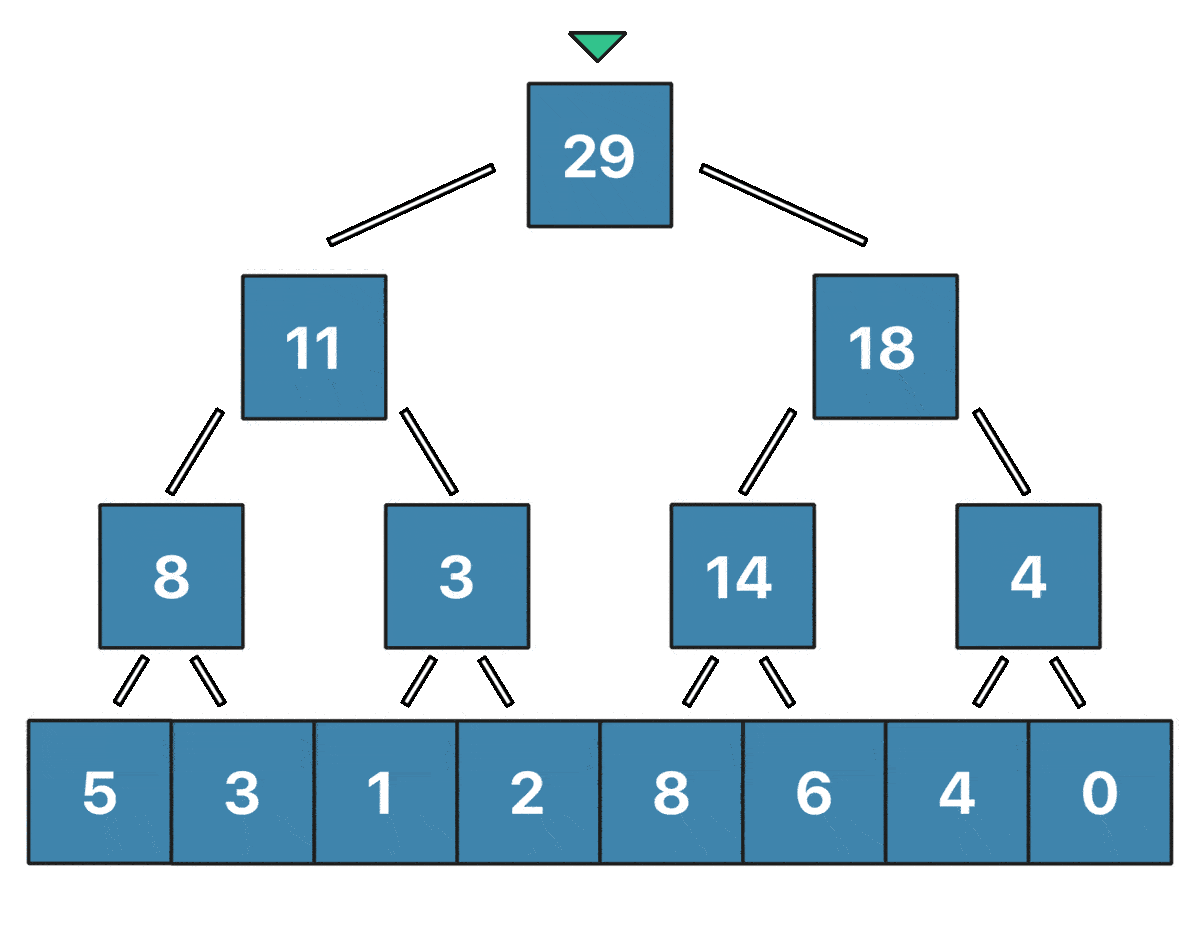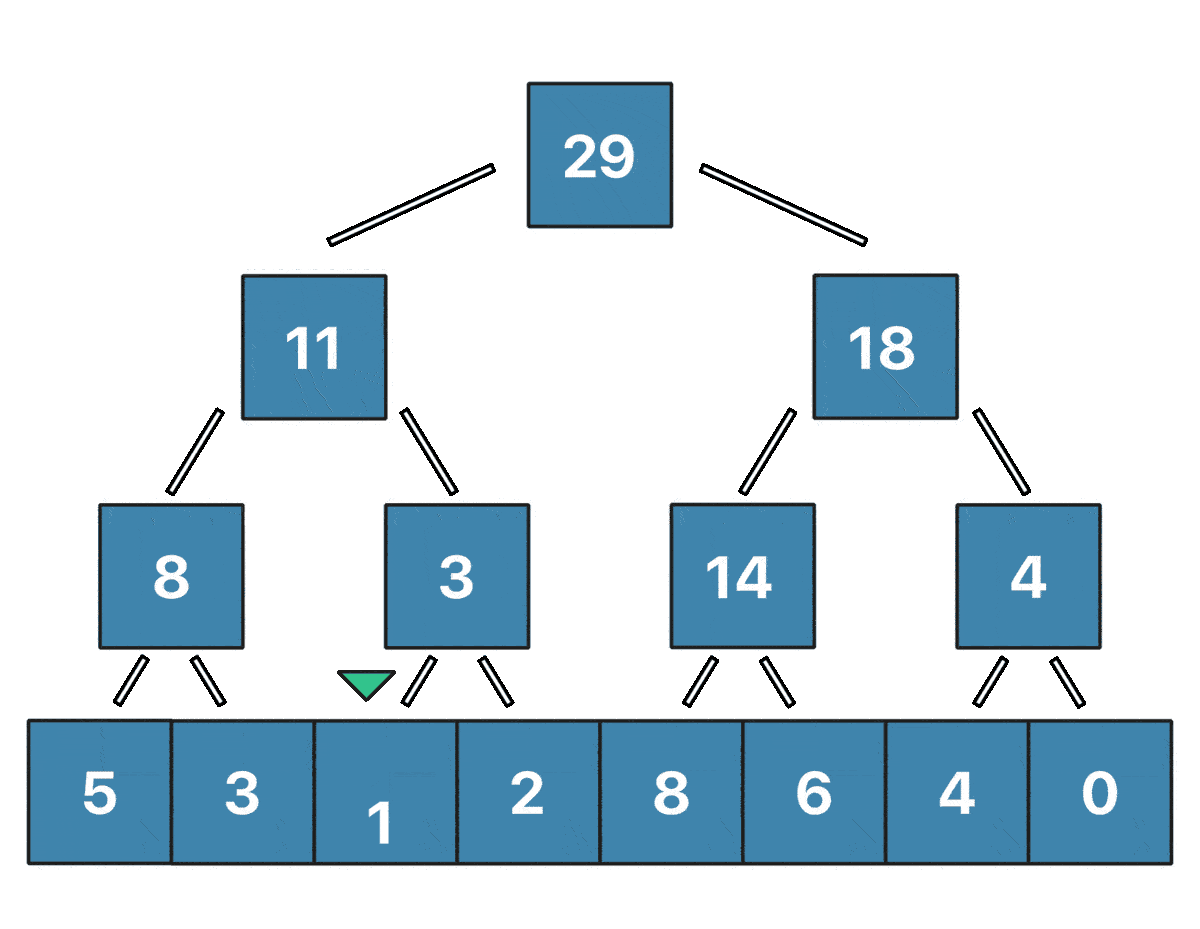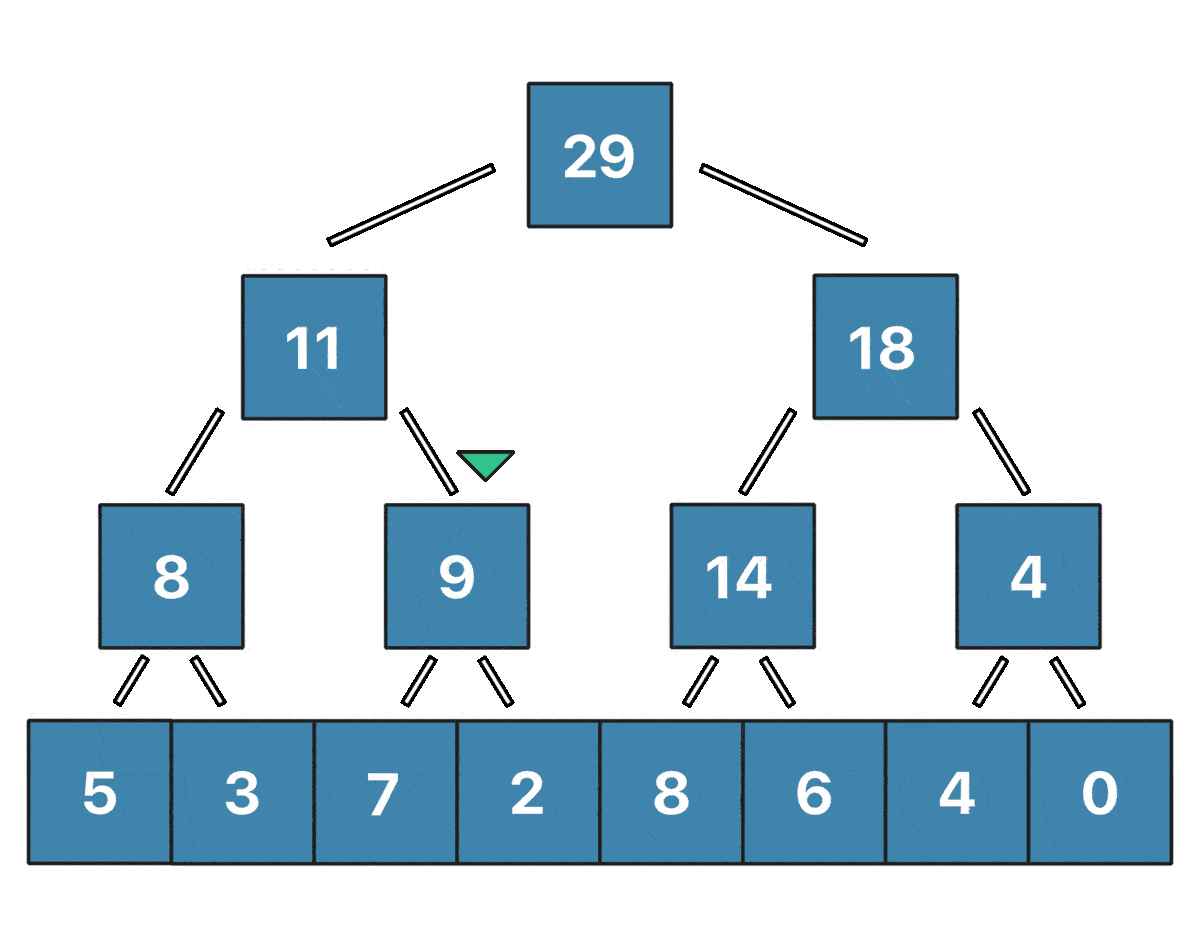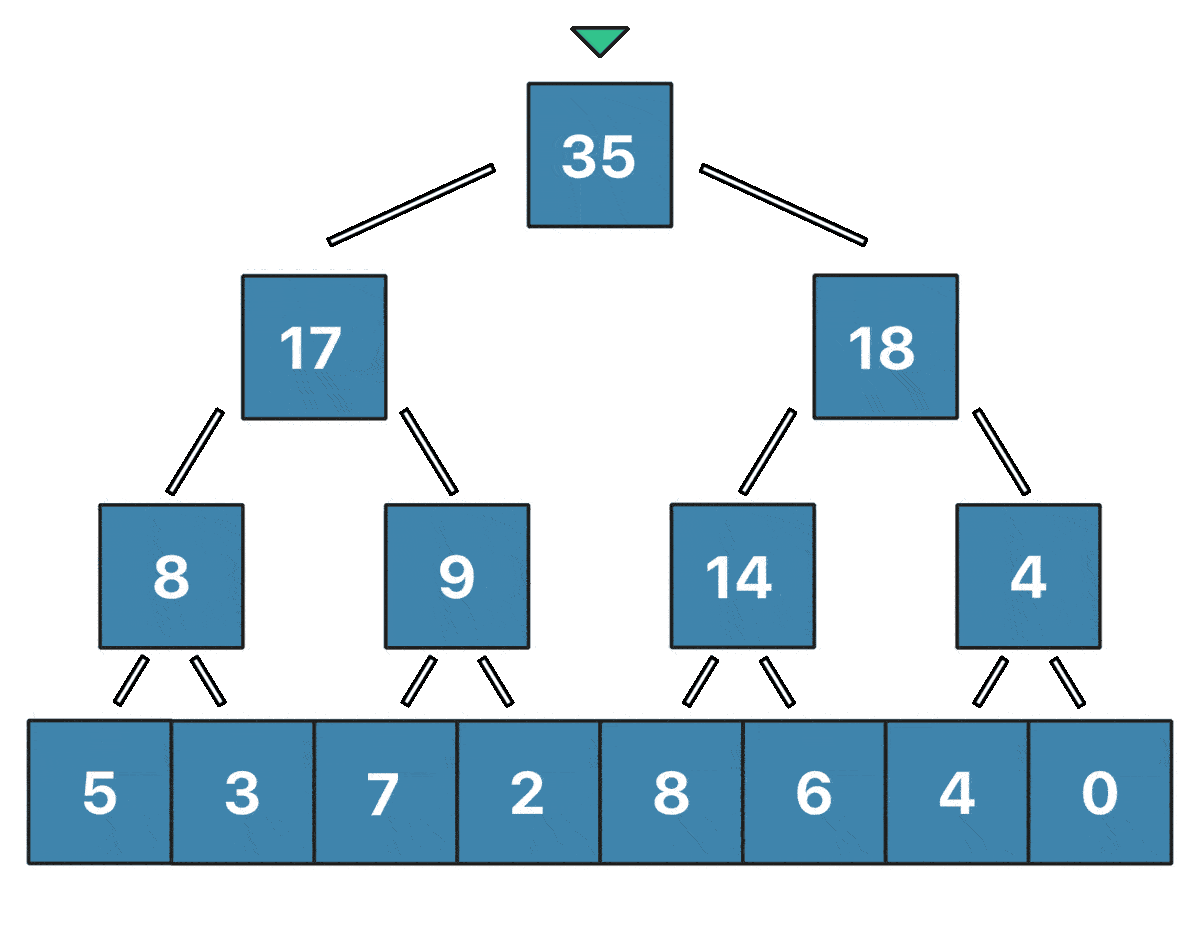
In the animation shown above, you can see the Update(i, v) in action.
Sum() Operation
Now let's see what the Sum() operation would look like on our segment tree. Notice how we already have all the values that we need to be stored in the nodes of our tree. In this case, the values are the sum of the segments in the original array.
Observe how the root already has the answer for a query from 0 to 8 which would be a perfect query, however, what happens if we have a nonperfect query like [2, 7)?
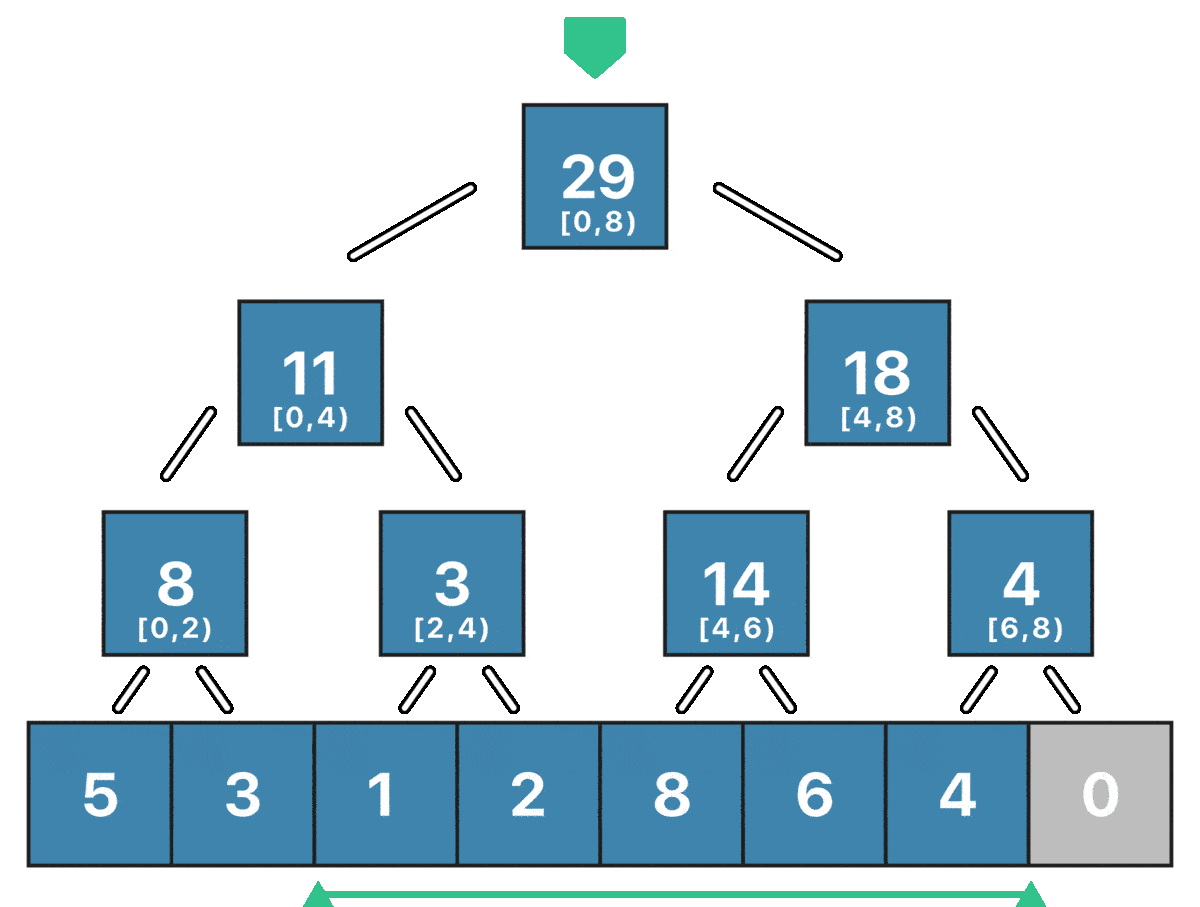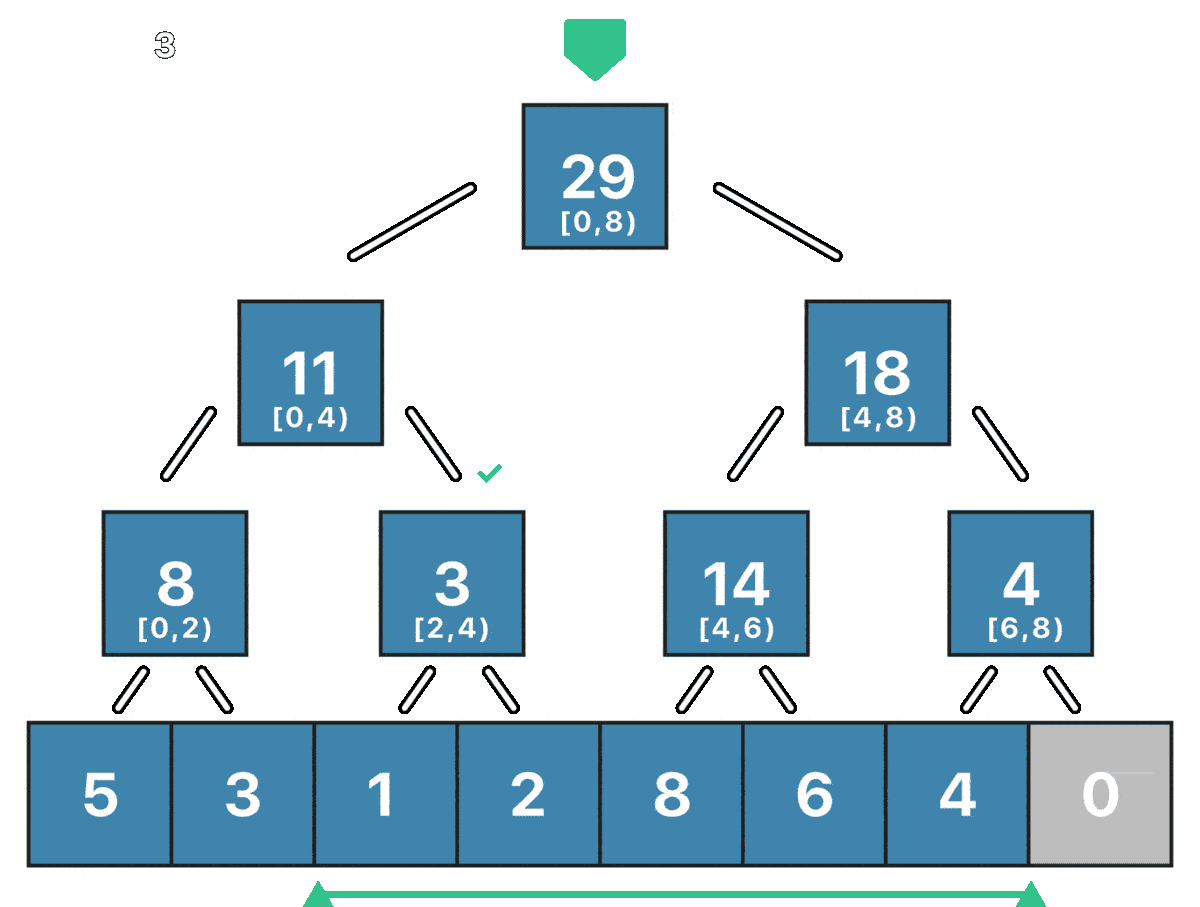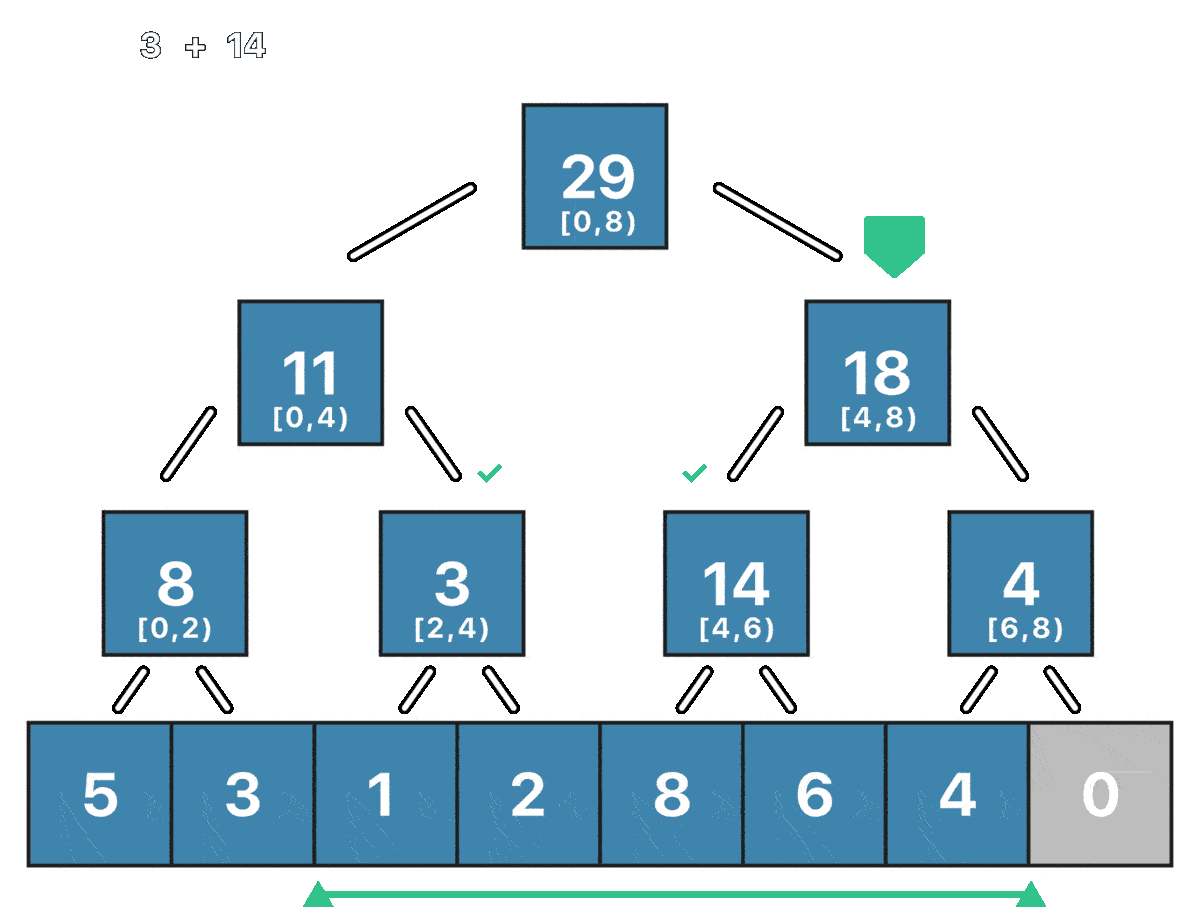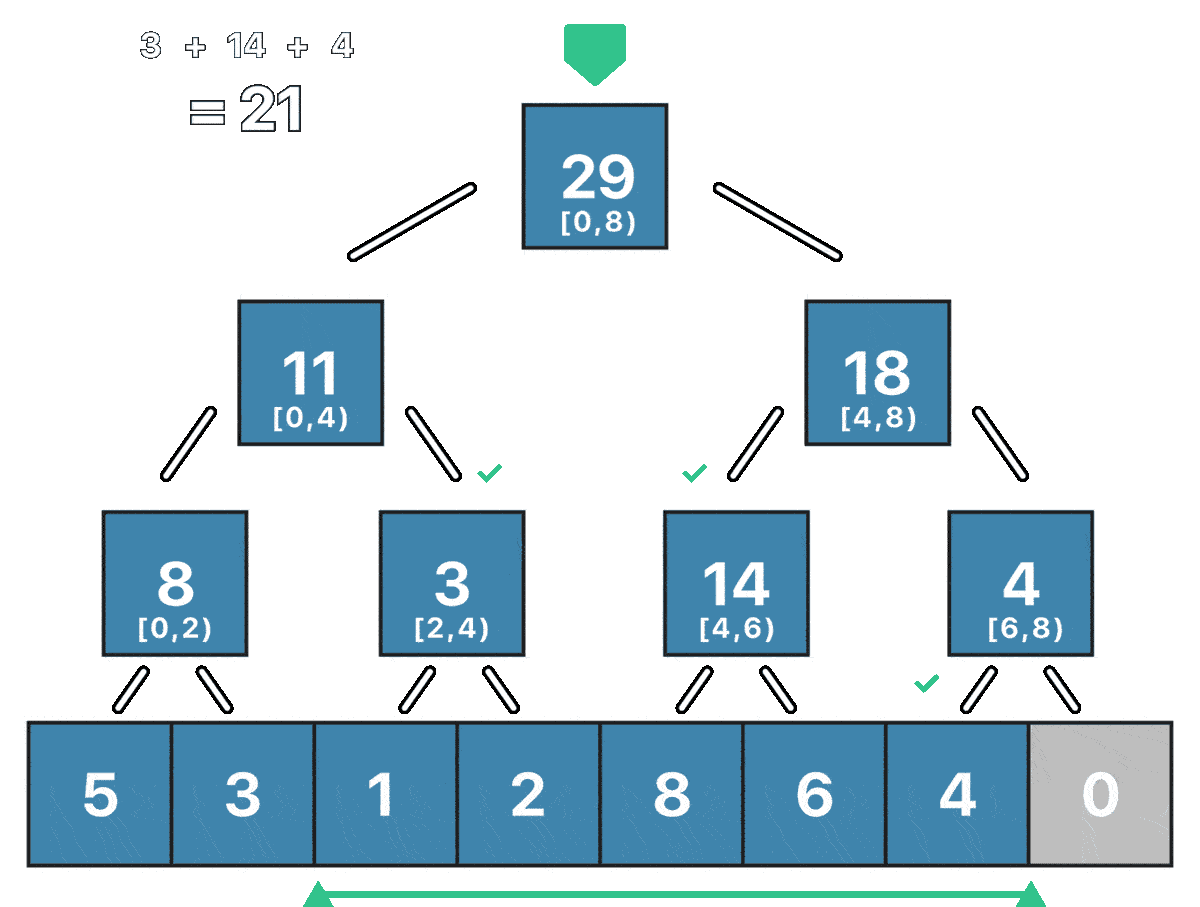
The algorithm will be a recursive traversal of the tree that will be interrupted by two cases.
- The segment corresponding to the current node is outside of the query, if this happens it means that all the children are outside of the desired query and we can stop the recursion.
- The segment corresponding to the current node is completely inside of the query, this means that all the children are inside of the range and we need to sum the value of the current node to our result and stop the recursion.
If the current node segment is partially inside the range query, then we simply continue traversing its children until one of both break cases happens.
Time - Space Complexity
Altho we haven't touched any of the code for this solution, you might already be thinking about if this solution is actually better than the iterative one, after all, it seems like there are a lot of more elements in our structure, and in the sum operation example, it might seem like there was more traversing and was slower than the other one, but is this really the case?
Segment Tree Space Complexity
if the array size N is a power of 2, then we have exactly n-1 internal nodes, summing up to 2n-1 total nodes. But not always do we have n as the power of 2, so we basically need the smallest power of 2 which is greater than n. For good measure, it's normally said that a Segment Tree has a space complexity of O(4n) which is manageable. If you want to dig a bit more about this topic I'll recommend you to check out this link
Update() Time Complexity
When performing the update operation, we need to recalculate one node on each layer of the tree. We have only logn layers, so the operation time will be O(logn).
Sum() Time Complexity
When performing the Sum() operation, we don't need to visit all the elements of the tree, thus the general asymptotic time of this procedure will be O(logn), way more efficient compared to the iterative solution.
When to use a segment tree?
Segment Trees are useful whenever you're frequently working with ranges of numerical data. We can use a segment tree if the function f is associative and the answer of an interval [l,r] can be derived from the data array. Here are some common examples:
- Find the sum of all values in a range
- Find the smallest value in a range
- Find the Max value in a rage
- Find the Product of all values in a Range (Multiplication)
- Bitwise operations
|&^
Implementing a Segment Tree with C++
In this section, we will look at how to implement the solution for the original sum problem using a genius Segment tree Array representation starting from the code template below.
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> arr(n);
for (auto &e : arr) cin >> e;
return 0;
}
Step 1 - Initializing Segment Tree
As you can see from the code cell below, we initialize two global variables, the segment tree size, and the base size.
int seg_tree_size, base_size;
vector<long long> segment_tree;
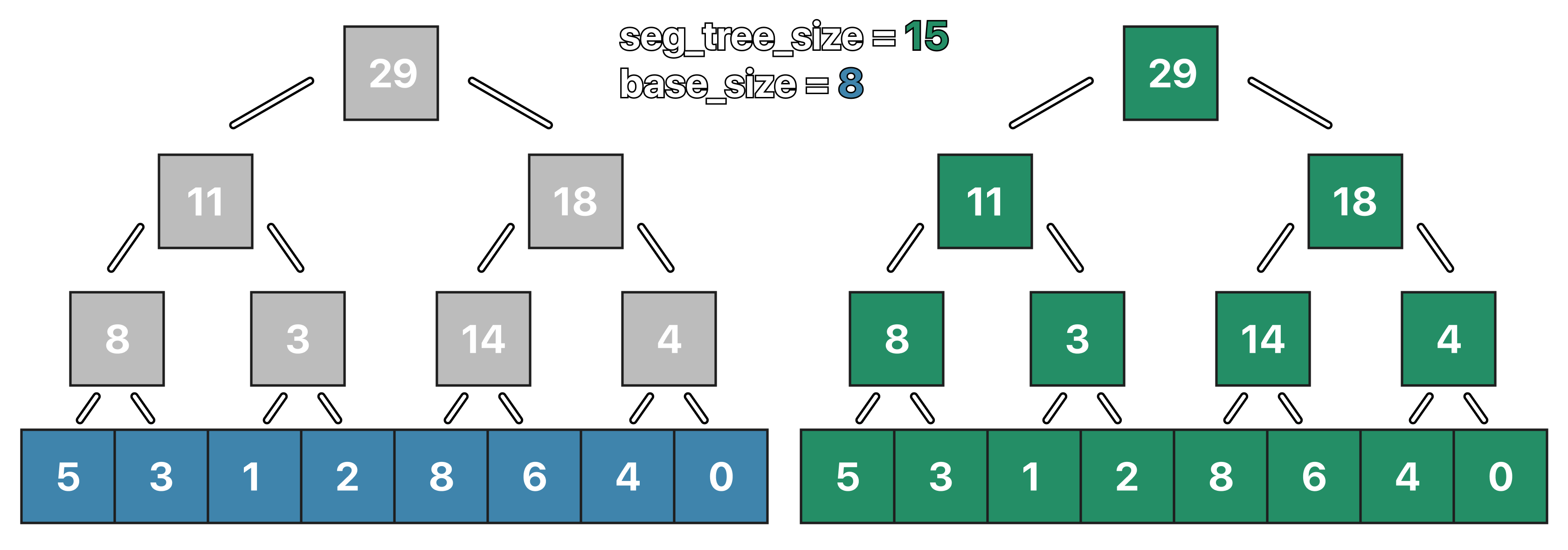
We also create our segment_tree that, as we mentioned earlier, it's going to be represented with an array, in this case, long long is the data type we use because we are going to be managing sums.
void init(const vector<int>& a) {
int arr_size = a.size();
base_size = 1;
while (base_size < arr_size) base_size *= 2;
seg_tree_size = base_size * 2 - 1;
segment_tree.resize(seg_tree_size, 0); // neutral value;
In the code cell above, you can see how we use a while loop, to find the smallest power of 2 which is greater than n in order to have a perfect binary tree. Now it's time to fill the tree leaves with the values of the original array.
for (int i = seg_tree_size / 2, j = 0; i < seg_tree_size && j < arr_size;
i++, j++) {
segment_tree[i] = a[j];
}
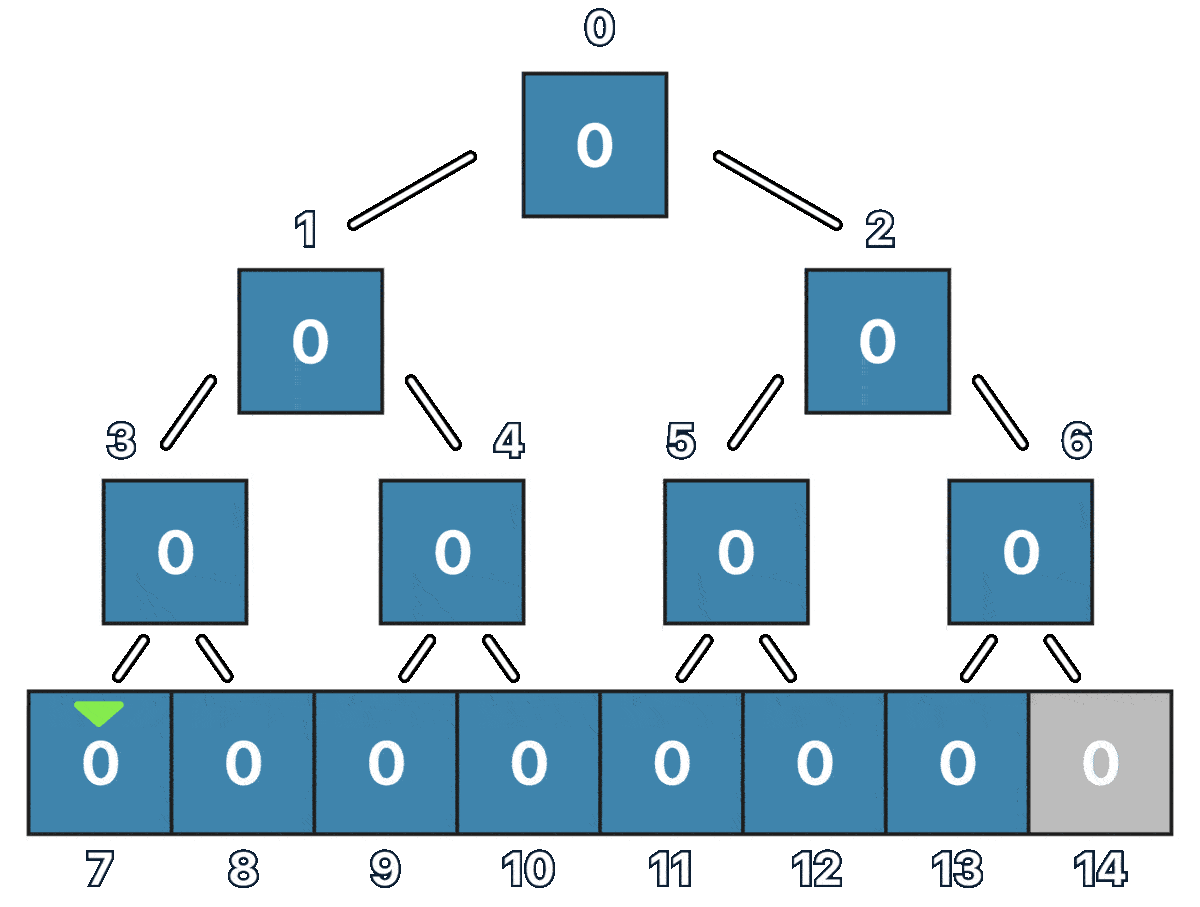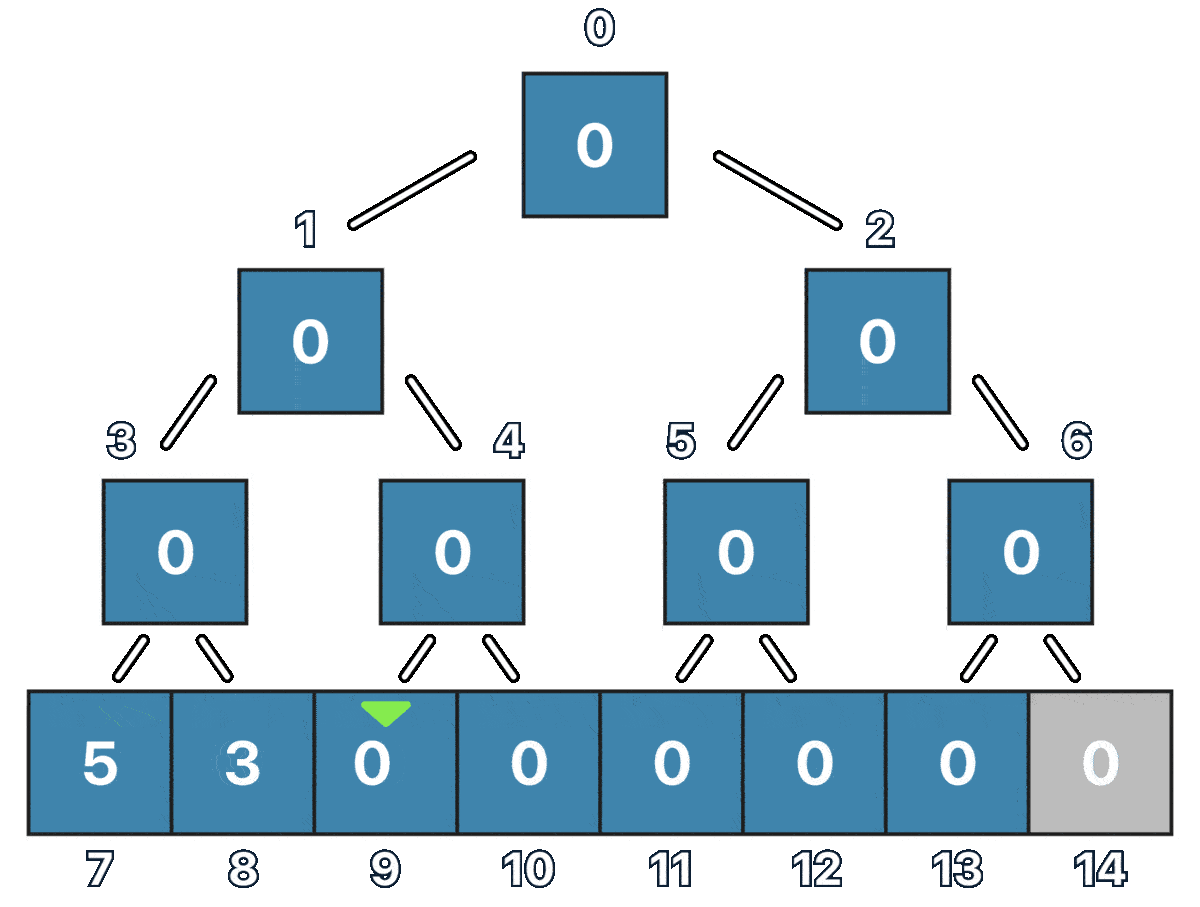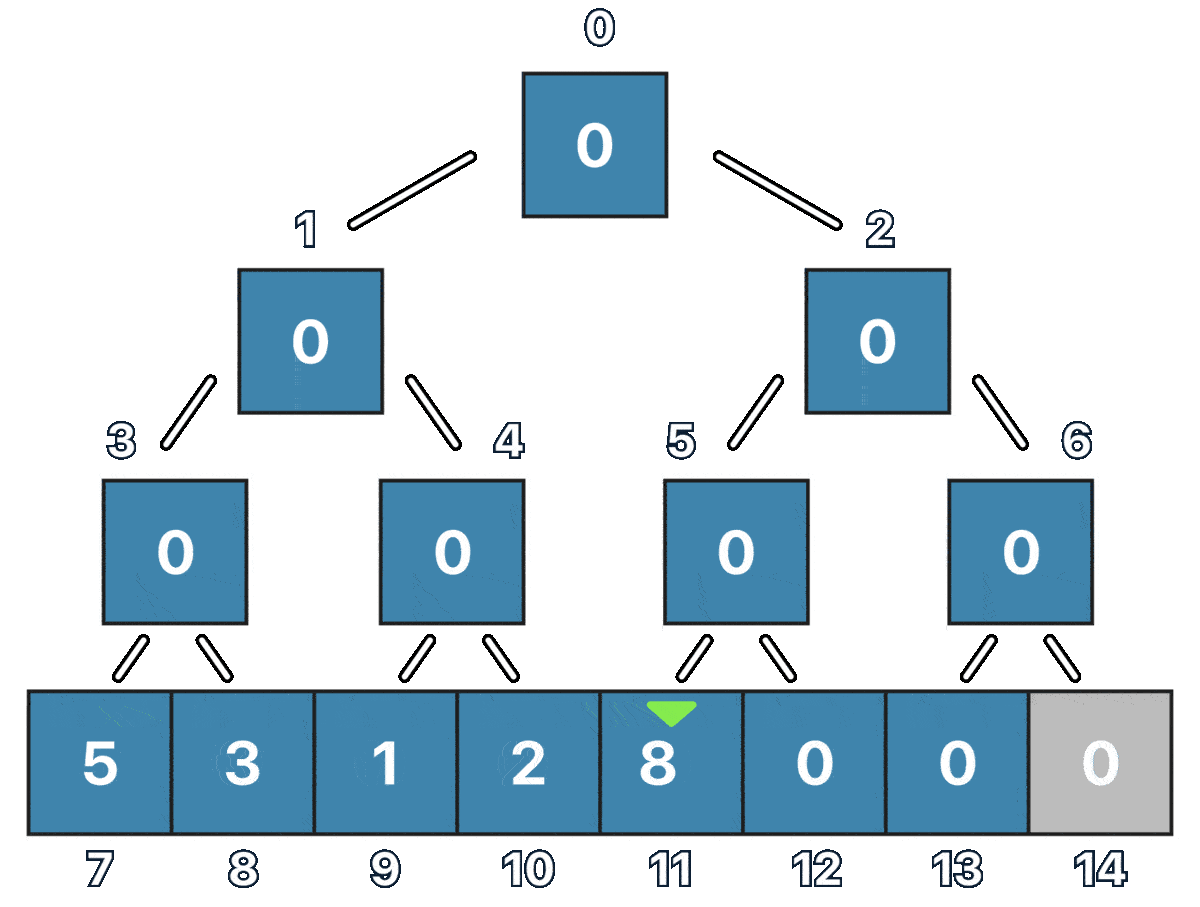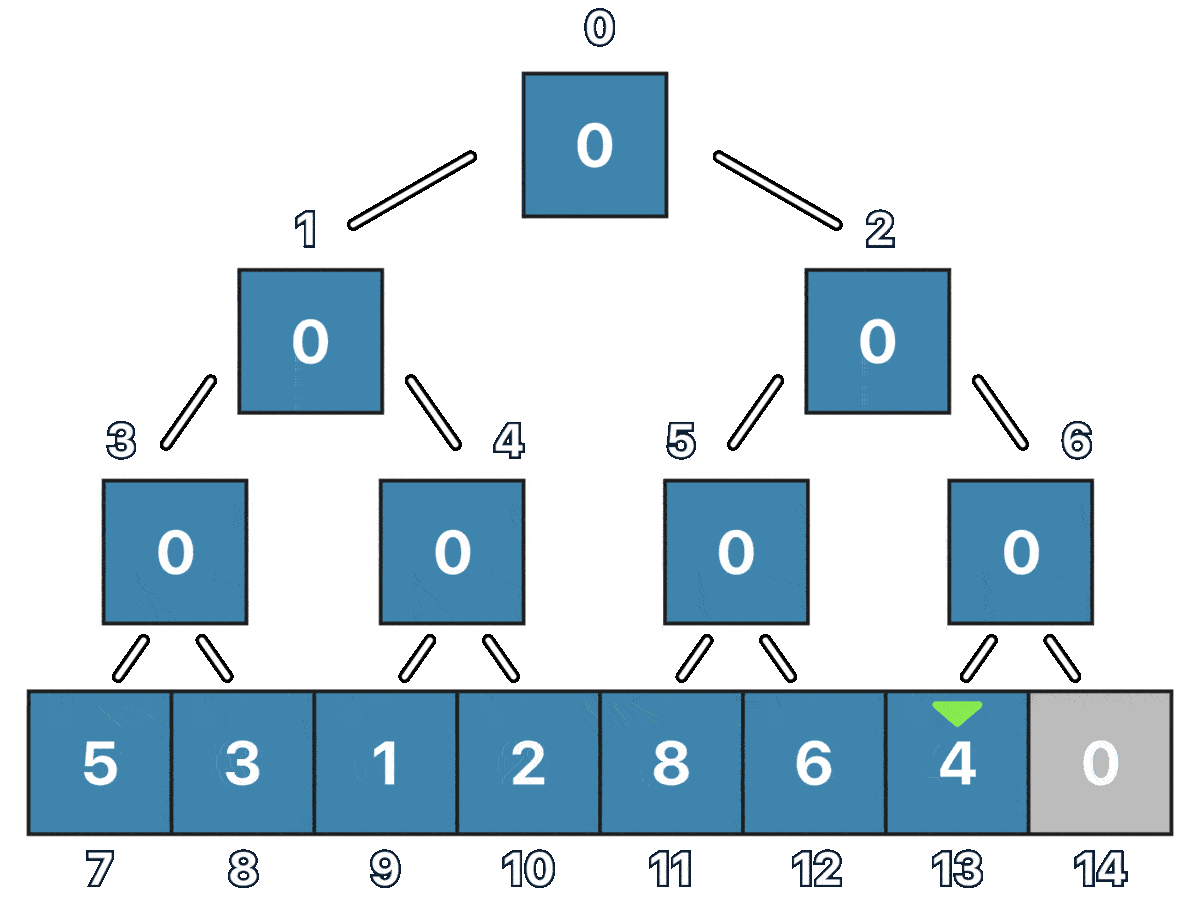Notice how we are representing the Tree as an array where each node has its index, and the furthest left leaf is always going to be the segment tree size divided by two.
Now that we filled all the leaves it's time to fill the rest of the tree
for (int i = seg_tree_size / 2 - 1; i >= 0; i--) {
segment_tree[i] = segment_tree[i * 2 + 1] + segment_tree[i * 2 + 2];
}
}
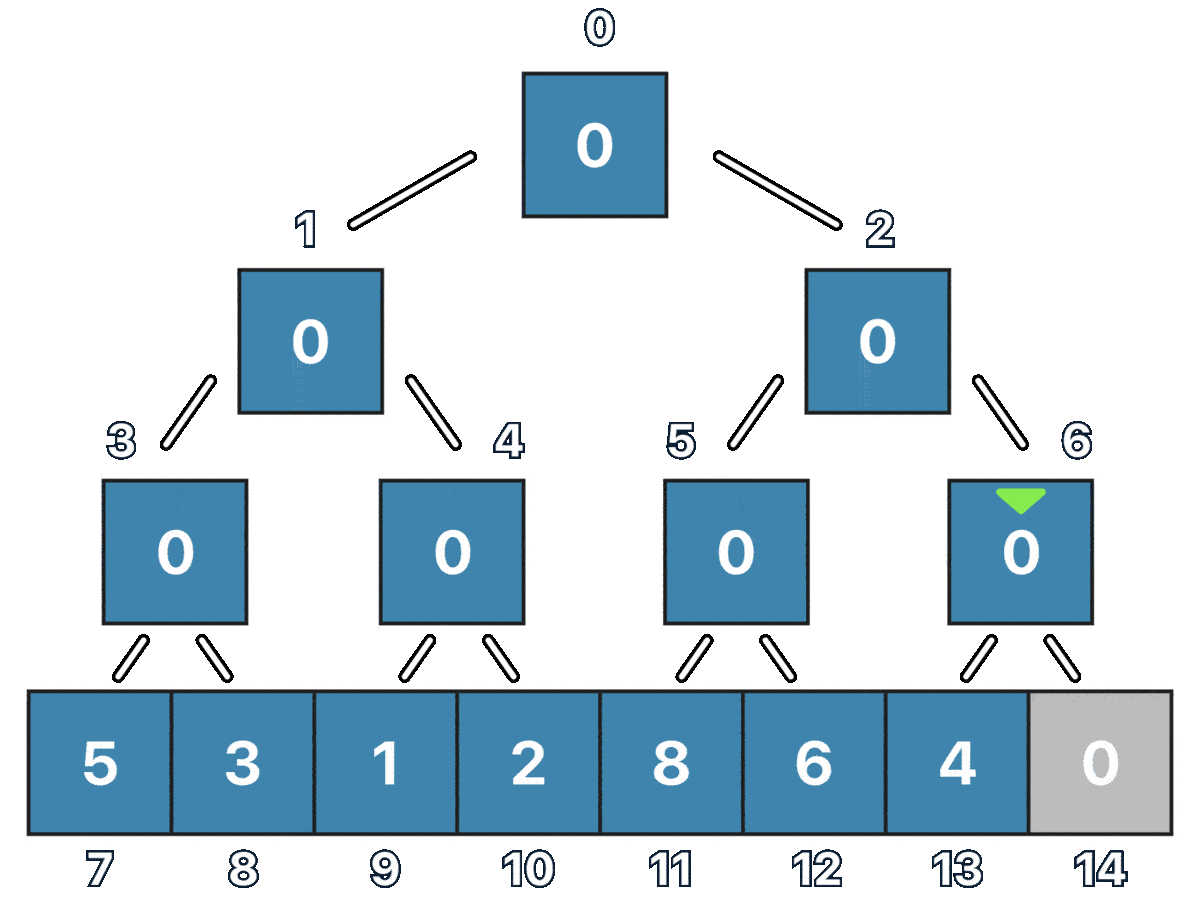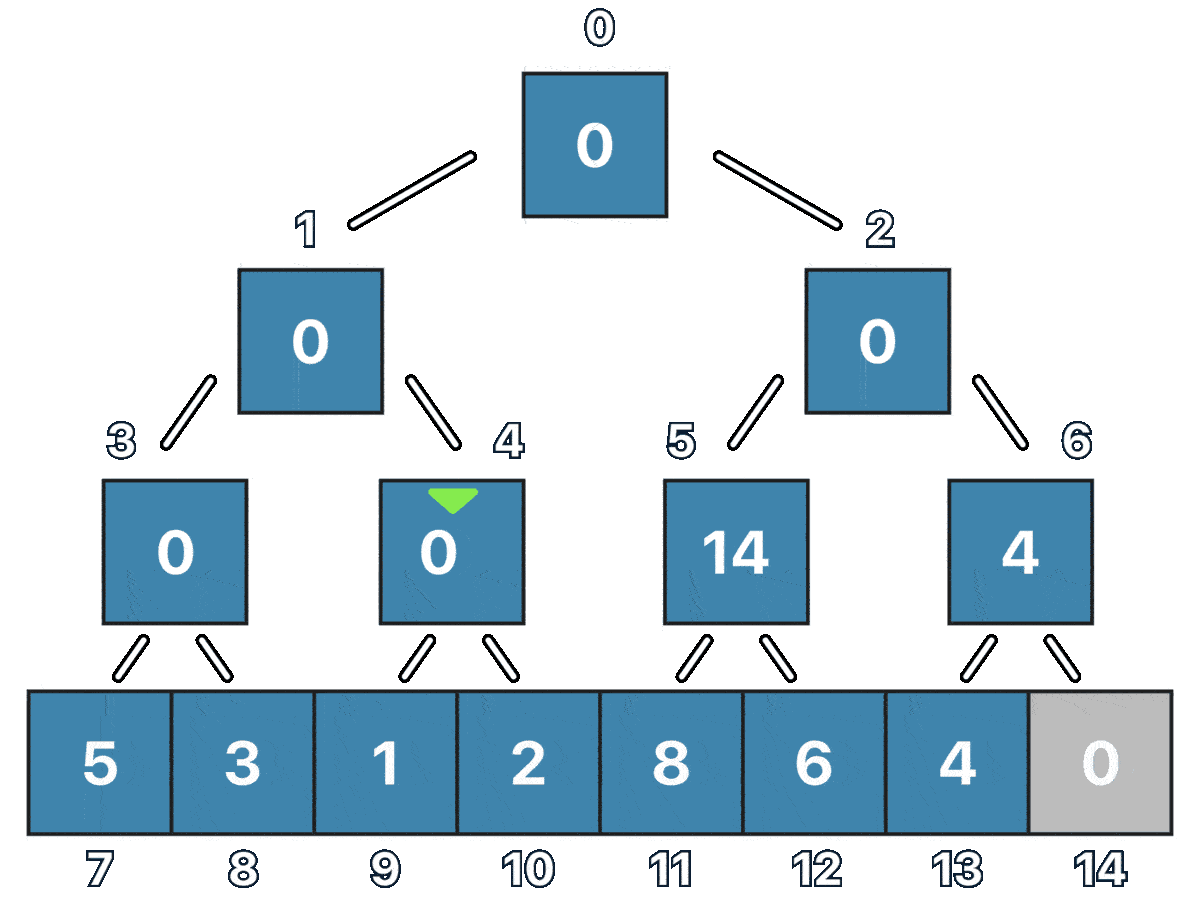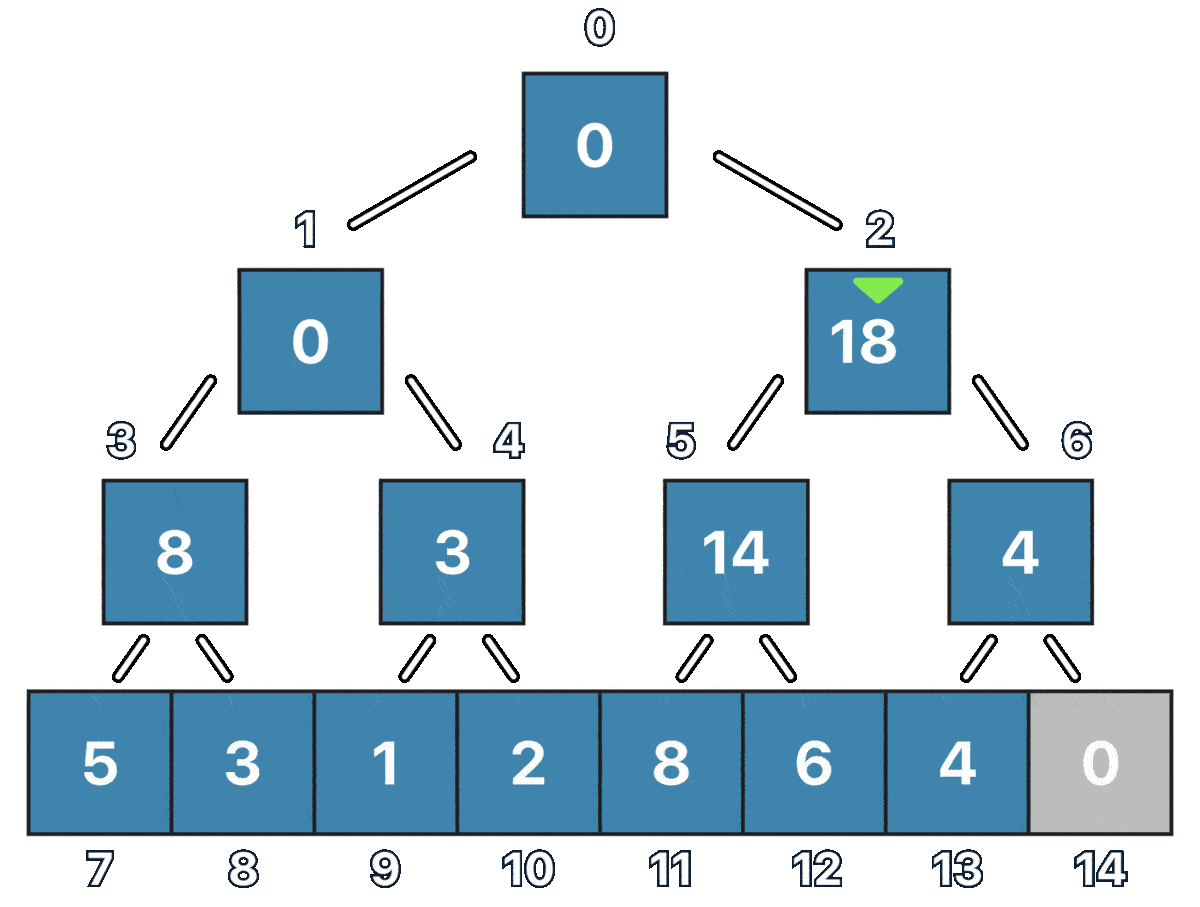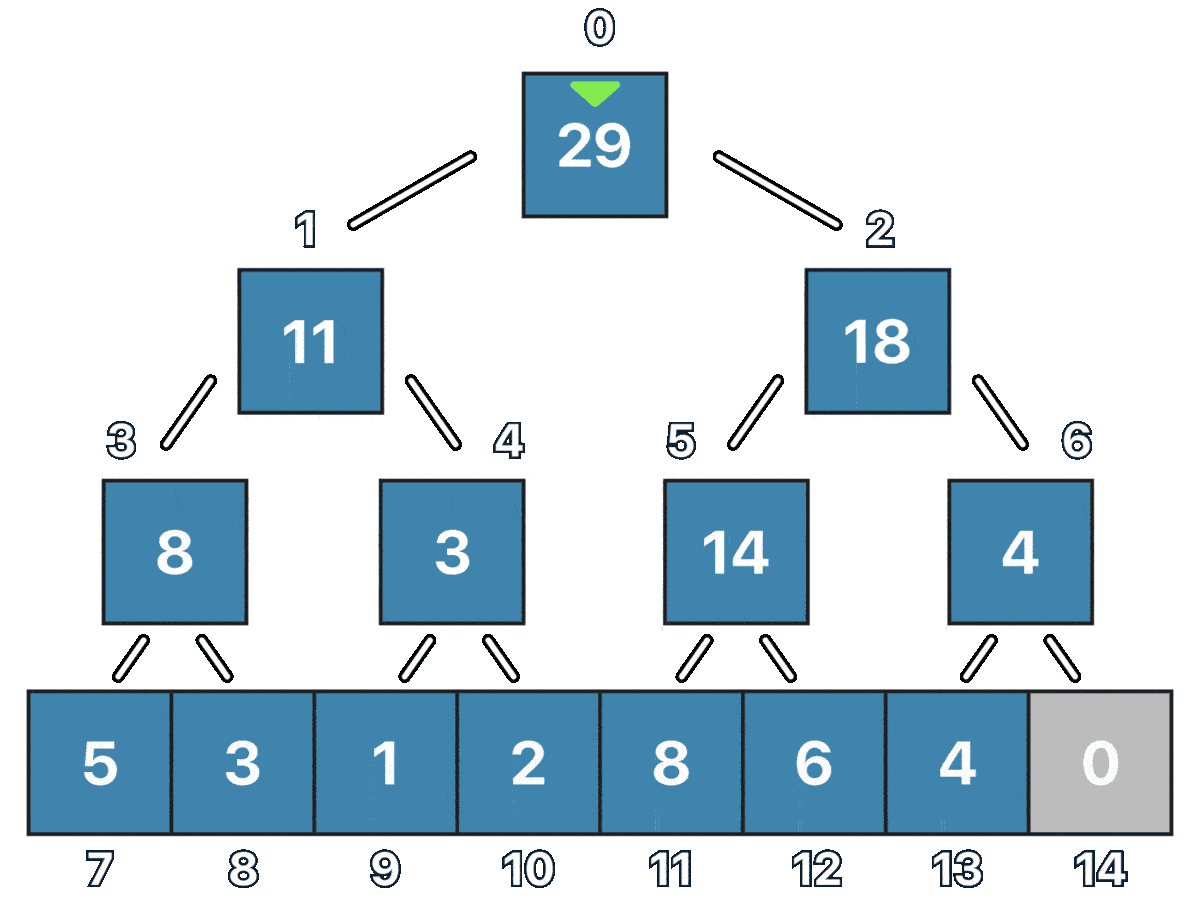
Notice how we start from the element in the (seg_tree_size / 2 - 1) position in this case the node at index 6, and thanks to the perfect binary tree that we have, we can easily check for both of its children with i * 2 + 1 and i * 2 + 2, In this particular case, we are making the node value to be the sum of both its children, this is normally what is adjusted for other associative properties.
Define update() Procedure
In case you forgot, this function is going to receive an index and a value, and update our array in the index to the new value. Thanks to our Array representation method we don't have to traverse the tree until we reach the desired node, instead, we just directly access the element with i += st_size / 2
void update(int i, int v) {
i += seg_tree_size / 2;
segment_tree[i] = v;
while (i > 0) {
i = (i - 1) / 2;
segment_tree[i] = segment_tree[i * 2 + 1] + segment_tree[i * 2 + 2];
}
}
Remember that once the value is updated, all the parent nodes to that leave have to be updated.
Define sum() Procedure
This recursive function shall take the query that is, [L and R), a helper left and right "searching" range and the index to the current node in the tree.
long long sum(int L, int R, int sl = 0, int sr = base_size, int i = 0) {
if (sl >= R || sr <= L) return 0; // Outside of range
if (sl >= L && sr <= R) return segment_tree[i]; // Inside of range
int mid = (sl + sr) / 2;
return sum(L, R, sl, mid, i * 2 + 1) + sum(L, R, mid, sr, i * 2 + 2);
}
Let's see what is happening here, in the first iteration we try to "search" the entire array, that's why sl is set to 0, and sr is set to the base_size, and we start on the root node, a.k.a the node at index 0.
The function will check if the searching range is outside of the query, if it is, we return 0, if instead, the searching range is completely inside of the query, we return the value of the segment tree node, else, it means that we are partially inside of the query, and because this is a binary tree, we can simply trim the search range in 2 with int mid = (sl + sr) / 2; and send the recursive function again to BOTH children.
Testing Solution + Full Code
#include <iostream>
#include <vector>
using namespace std;
int seg_tree_size, base_size;
vector<long long> segment_tree;
void init(const vector<int>& a) {
int arr_size = a.size();
base_size = 1;
while (base_size < arr_size) base_size *= 2;
seg_tree_size = base_size * 2 - 1;
segment_tree.resize(seg_tree_size, 0); // valor neutro;
for (int i = seg_tree_size / 2, j = 0; i < seg_tree_size && j < arr_size;
i++, j++) {
segment_tree[i] = a[j];
}
for (int i = seg_tree_size / 2 - 1; i >= 0; i--) {
segment_tree[i] = segment_tree[i * 2 + 1] + segment_tree[i * 2 + 2];
}
}
void update(int i, int v) {
i += seg_tree_size / 2;
segment_tree[i] = v;
while (i > 0) {
i = (i - 1) / 2;
segment_tree[i] = segment_tree[i * 2 + 1] + segment_tree[i * 2 + 2];
}
}
long long sum(int L, int R, int sl = 0, int sr = base_size, int i = 0) {
if (sl >= R || sr <= L) return 0; // Outside of range
if (sl >= L && sr <= R) return segment_tree[i]; // Inside of range
int mid = (sl + sr) / 2;
return sum(L, R, sl, mid, i * 2 + 1) + sum(L, R, mid, sr, i * 2 + 2);
}
int main() {
int n;
cin >> n;
vector<int> arr(n);
for (auto& e : arr) cin >> e;
init(arr); // <- DON'T FORGET TO CREATE THE SEGMENT TREE!
cout << sum(0, 7) << endl;
cout << sum(0, 1) << endl;
cout << sum(1, 6) << endl;
update(0, 10);
cout << sum(0, 7) << endl;
cout << sum(0, 1) << endl;
cout << sum(1, 6) << endl;
return 0;
}
Expected output:
29 5 20 34 10 20
Farewell - Conclusion
You've reached the end of this lesson on the Segment tree data structure, remember that this is a skill that takes a lifetime to master so don't feel frustrated if you don't get it right away because this isn't easy, but I really hope some of the guidelines we saw today were helpful and the basic foundations on this topic were well understood, remember, there is still a lot to learn and we definitively didn't cover everything on Segment Trees, but I hope this was a good beginner overview and that you grasped the concepts and feel more confident on your programming journey.
Let me know in the comments what you thought about this post and let me know what you will like to see next. See you in the next post, stay tuned!